Circular Functions
Whilst we may be more familiar with degrees, radians are more convenient to work with when doing calculus.
One radian is the angle subtended at the centre of a unit circle by an arc of 1 unit in length.
\[360^{\circ} = 2 \pi^{c}\]
Note: In general, we do not put any symbol to represent radians. Assume that all questions are in radians unless there is a degrees symbol. If a question is given to you in degrees, it should be answered in degrees.
In this chapter we deal with three functions - sine, cosine and tangent. In previous years, you will have been introduced to these to find the angle or side lengths in right angle triangles.
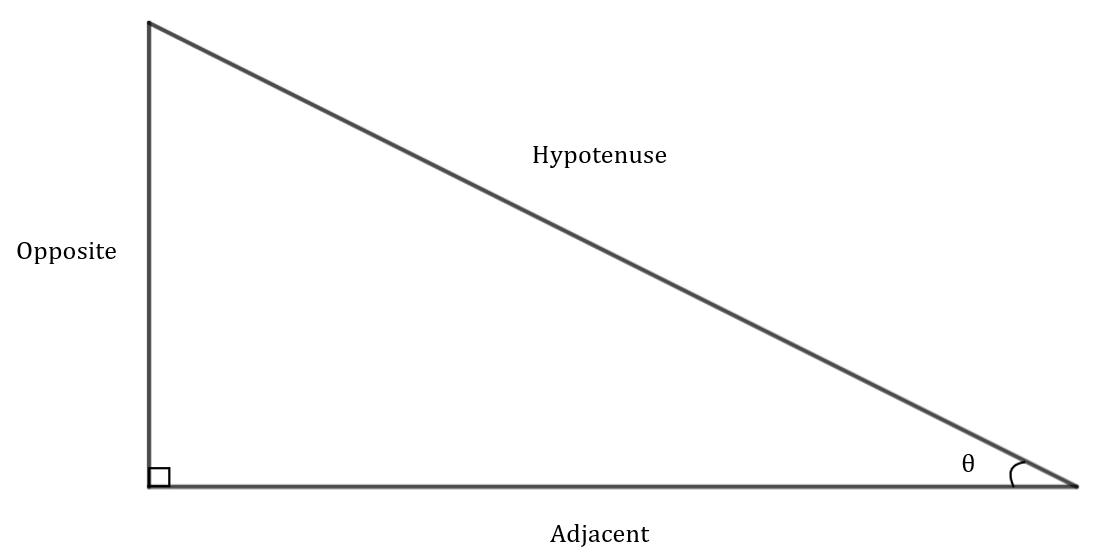
\[ \text{ } \\ \begin{aligned} \sin(\theta) &= \frac{\text{Opposite}}{\text{Hypotenuse}} \\ \text{ }\\ \cos(\theta) &= \frac{\text{Adjacent}}{\text{Hypotenuse}} \\ \text{ }\\ \tan(\theta) &= \frac{\text{Opposite}}{\text{Adjacent}} \\ \end{aligned}\\ \]
Looking at the first letter of each equation in that order we have:
SOH CAH TOA
A mnemonic which can be used to remember this is:
Some Old Hippy, Caught Another Hippy, Tripping On Acid.
While this knowledge is useful, we are now going to consider all angles, not only those in a right angled triangle.
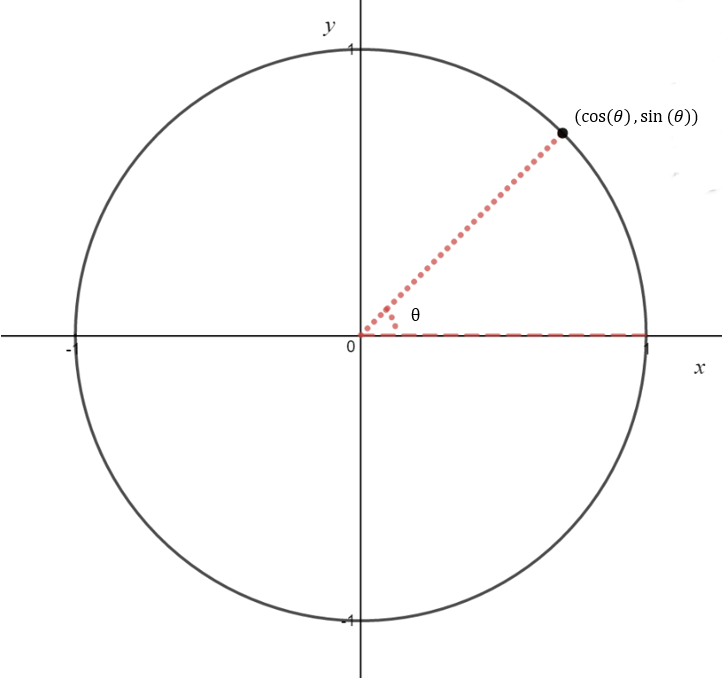
Above we have a circle with radius one. This is called the unit circle. The x-coordinate of any point on this circle is equal to \(\cos(\theta)\) and the y-coordinate of any point on this circle is equal to \(\sin(\theta)\). The angle theta is the angle going anti - clockwise from the red dashed line and any line from the edge of the circle to the origin as shown in the above diagram.
The tangent function is defined as the sine function divided by the cosine function. Because of this, whenever the cosine function is equal to zero, the tangent function is not defined. So in summary we have,
\[
\begin{aligned}
\sin(\theta) &= y \\
\text{ }\\
\cos(\theta) &= x \\
\text{ }\\
\tan(\theta) &= \frac{\sin(\theta)}{\cos(\theta)} \\
\text{ }\\
&= \frac{y}{x}
\end{aligned}
\]
Using these definitions, sine is positive in quadrant one and two, cosine is positive in quadrant one and four, and tangent is positive in quadrants one and three.
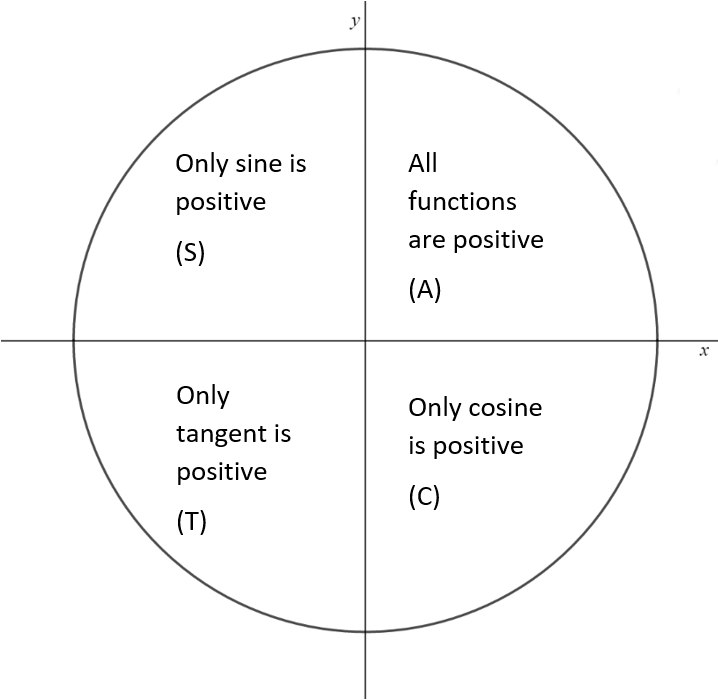
The easiest way to remember in which quadrants each function is negative or positive is simply remembering which quadrants the functions are positive. If you read clockwise from quadrant one (1,4,3,2) we spell ACTS.
A key property of circular functions is that they are periodic. If we look at the unit circle, if we add another \(360^{\circ}\) or \(2\pi\) to \(\theta\) you will end up at the same point. Thus, adding or subtracting \(2\pi\) to the argument (inside the brackets) of the sine, cosine and tangent functions will not change their value.
| \[\text{Radians}\] | \[0\] | \[\frac{\pi}{6}\] | \[\frac{\pi}{4}\] | \[\frac{\pi}{3}\] | \[\frac{\pi}{2}\] |
| \[\sin\] | \[0\] | \[\frac{1}{2}\] | \[\frac{\sqrt{2}}{2}\] | \[\frac{\sqrt{3}}{2}\] | \[1\] |
| \[\cos\] | \[1\] | \[\frac{\sqrt{3}}{2}\] | \[\frac{\sqrt{2}}{2}\] | \[\frac{1}{2}\] | \[0\] |
| \[\tan\] | \[0\] | \[\frac{\sqrt{3}}{2}\] | \[1\] | \[\sqrt{3}\] | \[\text{Undefined}\] |
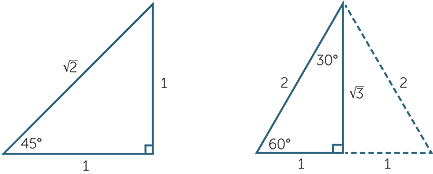
Knowing all of the exact values is imperative. However, memorising them is very difficult and not recommended! Simply remember the two triangles below. The one on the left is an isosceles triangle with the two equal sides being of length 1. The one on the right is an equilateral triangle with side lengths of 2 which has been cut in half. You can then use pythagoras’ theorem in both of these cases to find any missing side lengths.
Your teacher may have demonstrate how you can get all of the formulae below form the unit circle. We have found that the vast majority of students find this too complex and provides little help. Hence, this has not been explained.
| \[\sin(\pi - x) = \sin(x)\] | \[\cos(\pi - x) = -\cos(x)\] | \[\tan(\pi - x) = -\tan(x)\] |
| \[\sin(\pi + x) = -\sin(x)\] | \[\cos(\pi + x) = -\cos(x)\] | \[\tan(\pi + x) = \tan(x)\] |
| \[\sin( - x) = -\sin(x)\] | \[\cos( - x) = \cos(x)\] | \[\tan( - x) = -\tan(x)\] |
Note that adding \(2\pi\) to the argument on the left hand side will mean that the equalities still stand as the sine, cosine and tangent functions are periodic. For example:
\[\sin(3\pi-x) = \sin(\pi - x) = \sin(x)\]
There are 9 formulae above. Memorising each individual one is very difficult. Supplementary angle formulae involve various multiples of \(\pi\). This is how we recommend you get around memorising all the formulae. Let’s always assume that \(x\) is an angle between \(\frac{\pi}{2}\) and \(0\). In this case, \(\sin(x)\) and \(\cos(x)\) are always positive.
Using \(\sin(\pi-x)\) as an example, \(\pi-x\) would be located in quadrant two. Sine is positive in quadrant two, so, \(\sin(\pi-x)\) = \(\sin(x)\).
Using \(\cos(\pi+x)\) as an example, \(\pi+x\) would be located in quadrant three. Cosine is negative in quadrant three, so, \(\cos(\pi+x)\) = \(-cos(x)\).
Using \(\tan(2\pi-x)\) as an example, \(2\pi-x\) would be located in quadrant four. The tangent function is negative in quadrant four, so, \(\tan(2\pi-x)\) = -\(\tan(x)\).
Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. We have found that the vast majority of students find this too complex and provides little help. Hence, this has not been explained.
| \[\sin(\frac{\pi}{2}-x) = \cos(x)\] | \[\cos(\frac{\pi}{2}-x) = \sin(x)\] |
| \[\sin(\frac{\pi}{2}+x) = \cos(x)\] | \[\cos(\frac{\pi}{2}+x) = -\sin(x)\] |
| \[\sin(\frac{3\pi}{2}-x) =- \cos(x)\] | \[\cos(\frac{3\pi}{2}-x) =- \sin(x)\] |
| \[\sin(\frac{\pi}{2}-x) = -\cos(x)\] | \[\cos(\frac{\pi}{2}-x) = \sin(x)\] |
Note that adding \(2\pi\) to the argument on the left hand side will mean that the equalities still stand as the sine, cosine and tangent functions are periodic. For example:
\[\sin(\frac{5\pi}{2}-x) = \sin(\frac{\pi}{2}-x) = \cos(x)\]
There are 8 formulae above. Memorising each individual one is very difficult. Complementary angle formulae involve odd multiples of \(\frac{\pi}{2}\). This is how we recommend you get around memorising all the formulae. Again, let’s always assume that \(x\) is an angle between \(\frac{\pi}{2}\) and \(0\). In this case, \(\sin(x)\) and \(\cos(x)\) are always positive.
Using \(\sin(\frac{\pi}{2}-x)\) as an example, \(\frac{\pi}{2}\) would be located in quadrant one. Sine is positive in quadrant two, so, \(\sin(\frac{\pi}{2}-x) = \cos(x)\).
Using \(\frac{3\pi}{2}-x\) as an example, \(\frac{3\pi}{2}-x\) would be located in quadrant two. Cosine is negative in quadrant three, so, \(\cos(\frac{3\pi}{2}-x) =- \sin(x)\).
Note the difference between supplementary angle and complementary angle formulae. Supplementary angle formulae establish a relationship between the same circular functions and are relative to \(\pi\), while the complementary angle formulae establish a relationship between sine and cosine and are relative to \(\frac{\pi}{2}\).
\[\sin^2(\theta)+\cos^2(\theta)=1\]
\[ \text{Example 6.1: Given that } \sin(x)=-\frac{2}{5} \text{ where } x \in [\pi, \frac{3\pi}{2}), \text{ find } \cos(x) \text{ and }\tan(x).\\ \text{ }\\ \begin{aligned} \text{} \sin^2(x) + \cos^2(x) &= 1\\ \because \sin(x) &= -\frac{2}{5}\\ \therefore (-\frac{2}{5})^2 + \cos^2(x) &= 1\\ \cos^2(x) &= 1-\frac{4}{25}\\ \cos^2(x) &= \frac{21}{25}\\ \cos(x) &= \pm \sqrt{\frac{21}{25}}\\ \therefore \cos(x) &= -\frac{\sqrt{21}}{5}\quad \text{As }x \in [\pi, \frac{3\pi}{2})\\ \text{ }\\ \tan(x) &= \frac{\sin(x)}{\cos(x)}\\ \tan(x) &= -\frac{2}{5} \div -\frac{\sqrt{21}}{5}\\ \tan(x) &= \frac{2}{\sqrt{21}}\\ \end{aligned}\\ \]
The basic shape of circular functions are shown below.
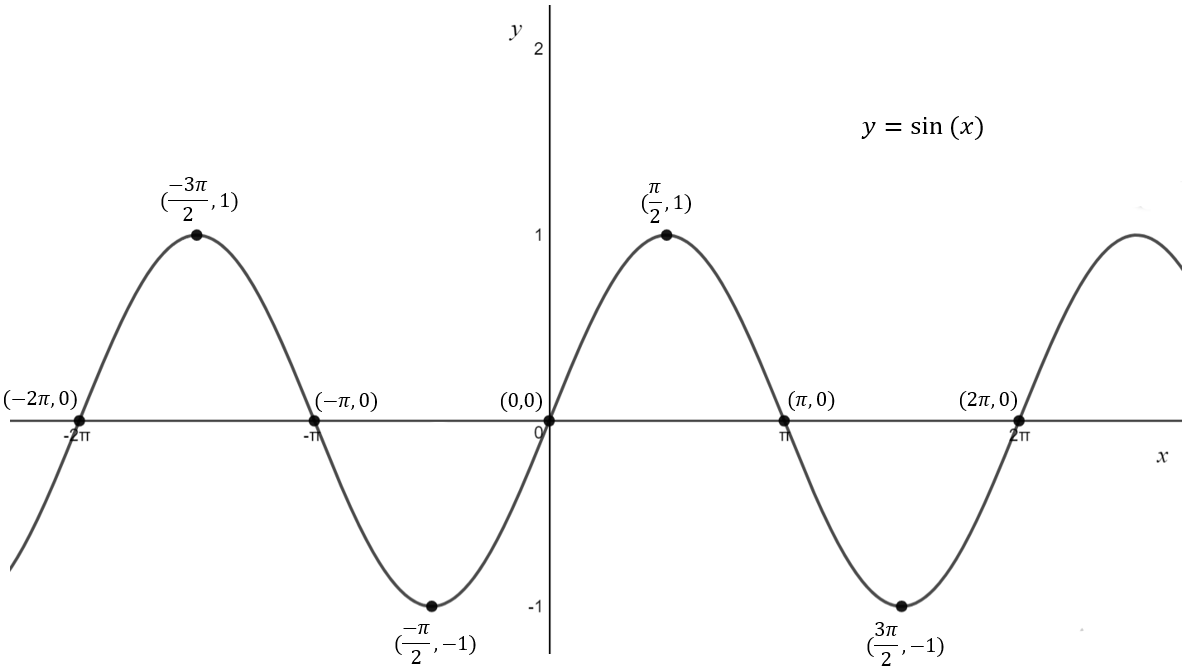


The amplitude of a function is the distance from the centreline (the horizontal line which lies in between the peaks and troughs) to the peak or trough. That is half the distance from the trough to peak.
The period is the interval (horizontal distance) between each repetition.
| Function | Amplitude | Period |
| \[y=A\sin(nx+b)+c \] | \[A\] | \[\frac{2\pi}{n}\] |
| \[y=A\cos(nx+b)+c \] | \[A\] | \[\frac{2\pi}{n}\] |
| \[y=A\tan(nx+b)+c \] | The tangent function does not have an amplitude | \[\frac{\pi}{n}\] |

A sine/cosine function is presented above. The length of the dotted vertical line is the amplitude. The length of the dotted horizontal line is the period.
In general, unless told not to, all graphs must provide the coordinates and equations of any: x-intercepts, y-intercepts and asymptotes.
\[y = A\sin(nx+b)+c \text{ and } y = A\cos(nx+b)+c\]
| 1 | Substitute x = 0 into the equation and solve for y to find the y-intercept |
| 2 | Write down the range, period and equation of the centreline (the horizontal line which lies in between the peaks and troughs) this is whatever the value c is. |
| 3 | Substitute y = 0 into the equation and solve for x to find the x-intercepts. Remember to take note of the domain provided in the question. |
| 4 | Find a value of x within the domain for when \(\sin(nx+b)=1\) or \(\cos(nx+b)=1\). Let’s call that point d. Mark in the coordinate \((d,A+c)\) |
| 5 | Add or subtract the period of the graph from d until you get outside of the domain. All of those points obtained will have the y-coordinate \((A+c)\). They will lie on the same horizontal line as the point graphed in step 4. Theses are the peaks (troughs). |
| 6 | Pick any point hat you graphed in steps 4 or 5 and add or subtract half a period to the x-coordinate, making sure that the new value is still inside the domain. Let’s call that point e. This is when \(\sin(nx+b) = -1\) or \(\cos(nx+b)\) Mark in the coordinate \((e,-A+c)\) |
| 7 | Add or subtract the period of the graph from e until you get outside of the domain. All of those points obtained will have the y-coordinate \((-A+c)\). They will lie on the same horizontal line as the point graphed in step 6. Theses are the troughs (peaks). |
| 8 | Calculate the coordinates of the endpoints. |
| 9 | Connect the dots appropriately and label the graph. |
\[y = A\tan(nx+b)+c\]
| 1 | Substitute x = 0 into the equation and solve for y to find the y-intercept |
| 2 | Substitute y = 0 into the equation and solve for x to find the x-intercepts. Remember to take note of the domain provided in the question. |
| 3 | Solve \(\cos(nx+b) = 0 \) for \(x\). This is where asymptotes will lie. |
| 4 | For any two asymptotes directly next to each other, find the midpoint. Let this value be d. Dot in the point (d,c). Do this for every pair of asymptotes directly next to each other. These points are the stationary points of inflection. |
| 5 | Find the coordinates of the endpoints |
| 6 | Connect up the dots and label the graph. Note that If \(A>0\), the graph will start in the bottom left corner and move to the top right corner (in between two asymptotes which are next to each other). Alternatively, If \(A<0\), the graph will start in the top left corner and move to the bottom right corner (in between two asymptotes which are next to each other). |
\[
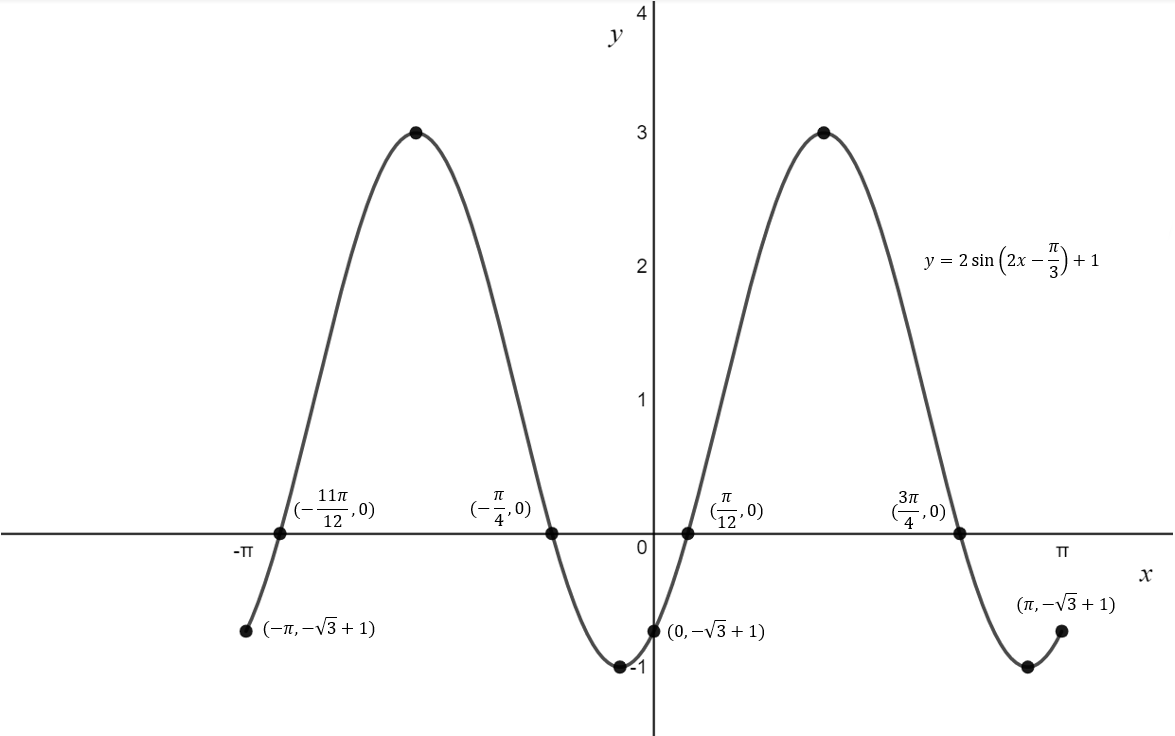
\text{Example 6.2: Sketch the graph of } y = 2\sin(2x-\frac{\pi}{3})+1 \text{ for } x \in [-\pi, \pi].\\
\text{Label the coordinates of any y-intercept, x-intercept or endpoint.}
\]
\[
\text{1. y-intercept} \\
\begin{aligned}
x&=0\\
y &= 2\sin(2\cdot 0-\frac{\pi}{3})+1 \\
y &= 2\sin(-\frac{\pi}{3}) + 1 \\
y&= 2 \cdot -\frac{\sqrt{3}}{2} + 1 \\
y&= -\sqrt{3} + 1 \\
\end{aligned}\\
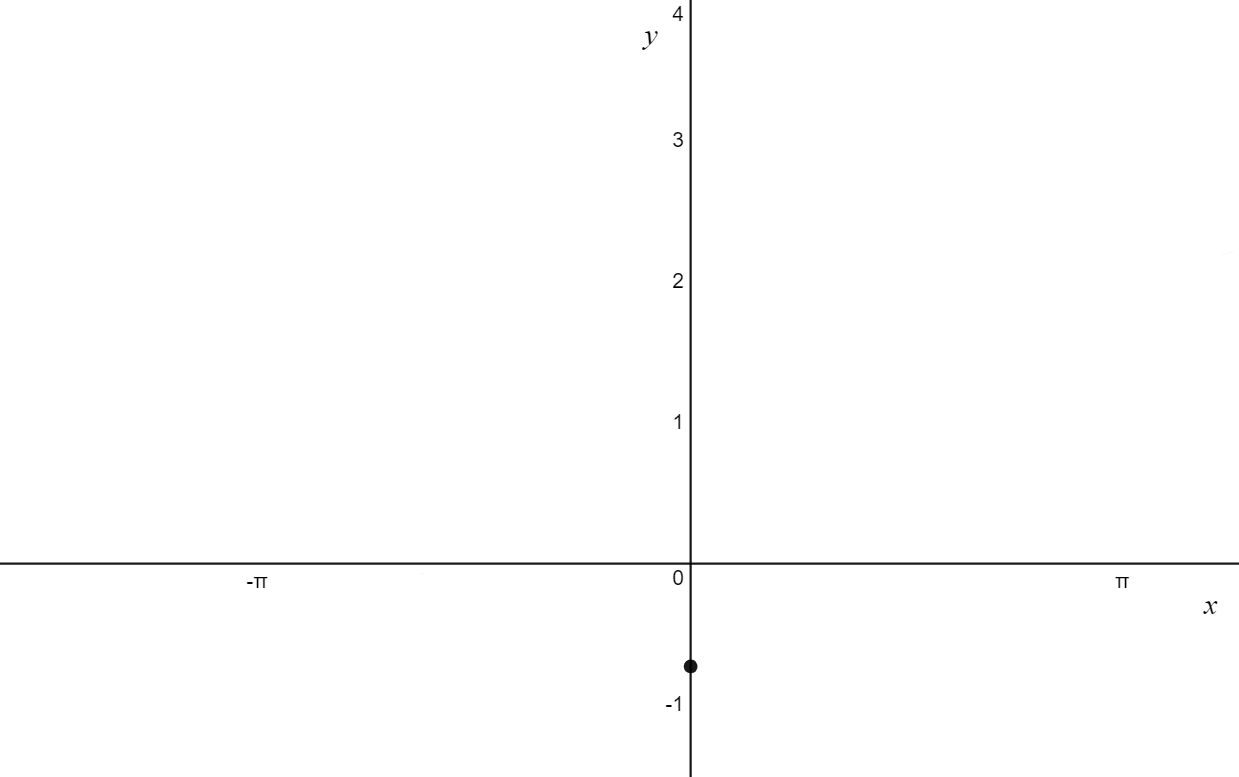
\text{There is a y-intercept at } (0, -\sqrt{3} + 1) \\
\]
\[
\text{2. Range, period and centreline} \\
\text{Range : } [1,3] \\
\text{Period: } \frac{2\pi}{2} = \pi \\
\text{Centreline: } y = 1 \\
\]
\[
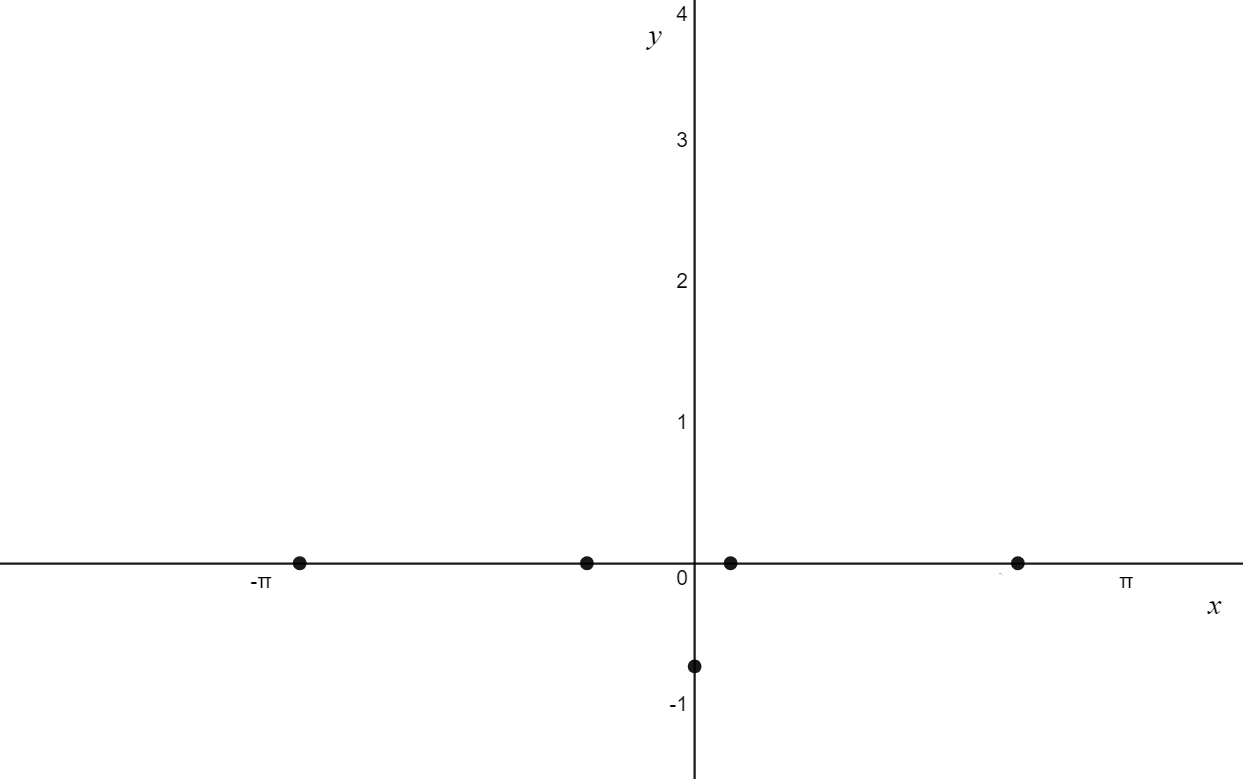
\text{3. x-intercepts} \\
\text{For working, please view the “Solving circular functions” example, it is the exact same question} \\
x = -\frac{11\pi}{12}, \,-\frac{\pi}{4},\,\frac{\pi}{12}\,\frac{3\pi}{4} \\
\text{There are x-intercepts at: } (-\frac{11\pi}{12},0), \,(-\frac{\pi}{4},0), \,(\frac{\pi}{12},0),\,(\frac{3\pi}{4},0)
\]
\[
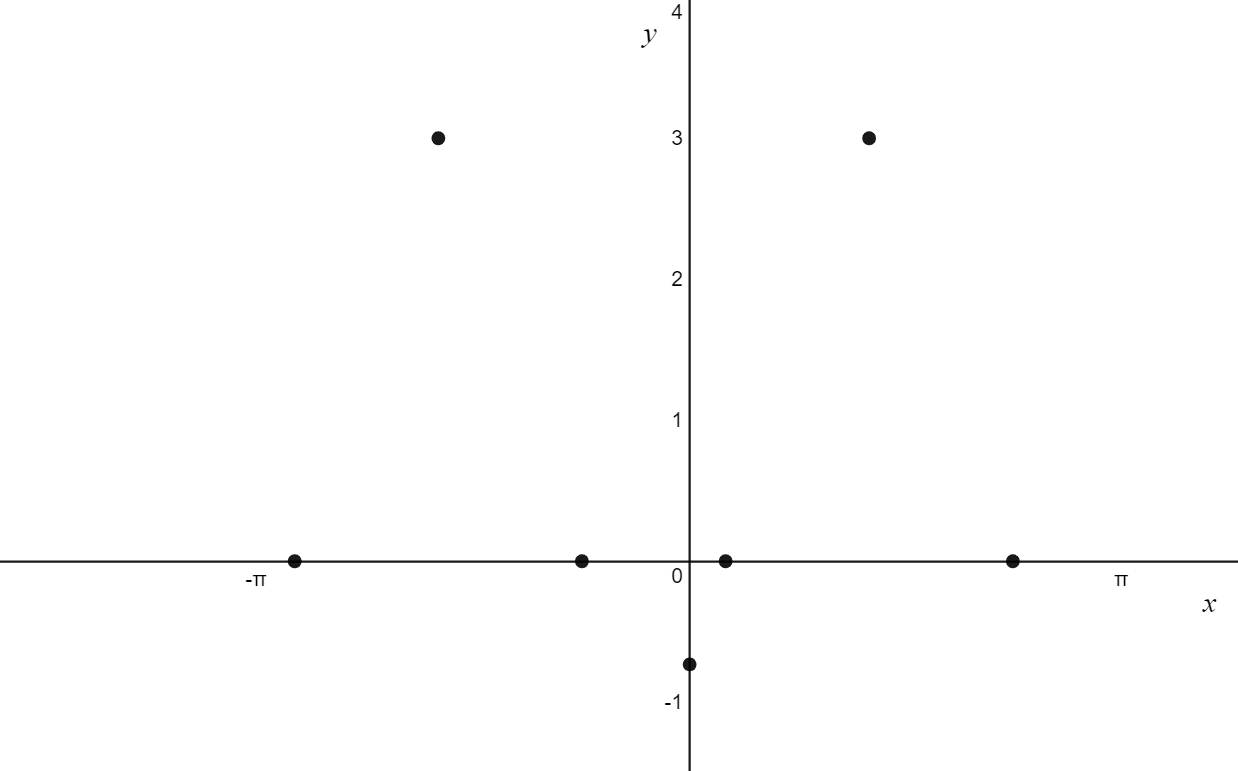
4. \, \sin(nx+b) = 1\\
\begin{aligned}
x&\in[-\pi,\pi]\\
2x&\in[-2\pi,2\pi] \\
\sin(2x-\frac{\pi}{3}) &=1 \\
\text{Basic Angle: }& \frac{\pi}{2} \\
\text{Let, } 2x-\frac{\pi}{3} &= \frac{\pi}{2} \\
2x&=\frac{5\pi}{6} \\
x&=\frac{5\pi}{12} \\
\text{ }&\\
\sin(2x-\frac{\pi}{3})=1 \, &\rightarrow \, 2\sin(2x-\frac{\pi}{3}) + 1 = 3 \\
\end{aligned}\\
\text{so, the point } (\frac{5\pi}{12}, 3) \text{ lies on our graph}
\]

\[
\text{5. Add or subtract the period from the x-coordinate in step 4} \\
\text{Period: } \pi \\
\text{Adding or subtracting } \pi \text{ from } \frac{5\pi}{12} \text{ we get:} \\
-\frac{7\pi}{12} \\
\text{All other values are outside of the domain} \\
\text{so, the point } (-\frac{7\pi}{12}, 3) \text{ lies on our graph}
\]
\[
\text{6. Add or subtract half a period from the x-coordinate of one of the points in step 4 or 5} \\
\text{We will add half a period to the x-coordinate of the point found in step 5. \\
allowing the x-value to still be in the domain} \\
\text{Half a period: } \frac{\pi}{2} \\
-\frac{7\pi}{12} + \frac{\pi}{2} = -\frac{\pi}{12} \\
\text{At this point } \sin(2x-\frac{\pi}{3}) = -1 \\
\begin{aligned}
\text{so, } y &= 2 \cdot (-1) + 1 \\
y &= -1 \\
\end{aligned}\\
\text{Thus, the point } (-\frac{\pi}{12}, -1) \text{ lies on our graph}
\]

\[
\text{7. Add or subtract the period from the x-coordinate in step 6} \\
\text{Period: } \pi \\
\text{Adding or subtracting } \pi \text{ from } -\frac{\pi}{12} \text{ we get:} \\
\frac{11\pi}{12} \\
\text{All other values are outside of the domain} \\
\text{so, the point } (\frac{11\pi}{12}, -1) \text{ lies on our graph}
\]
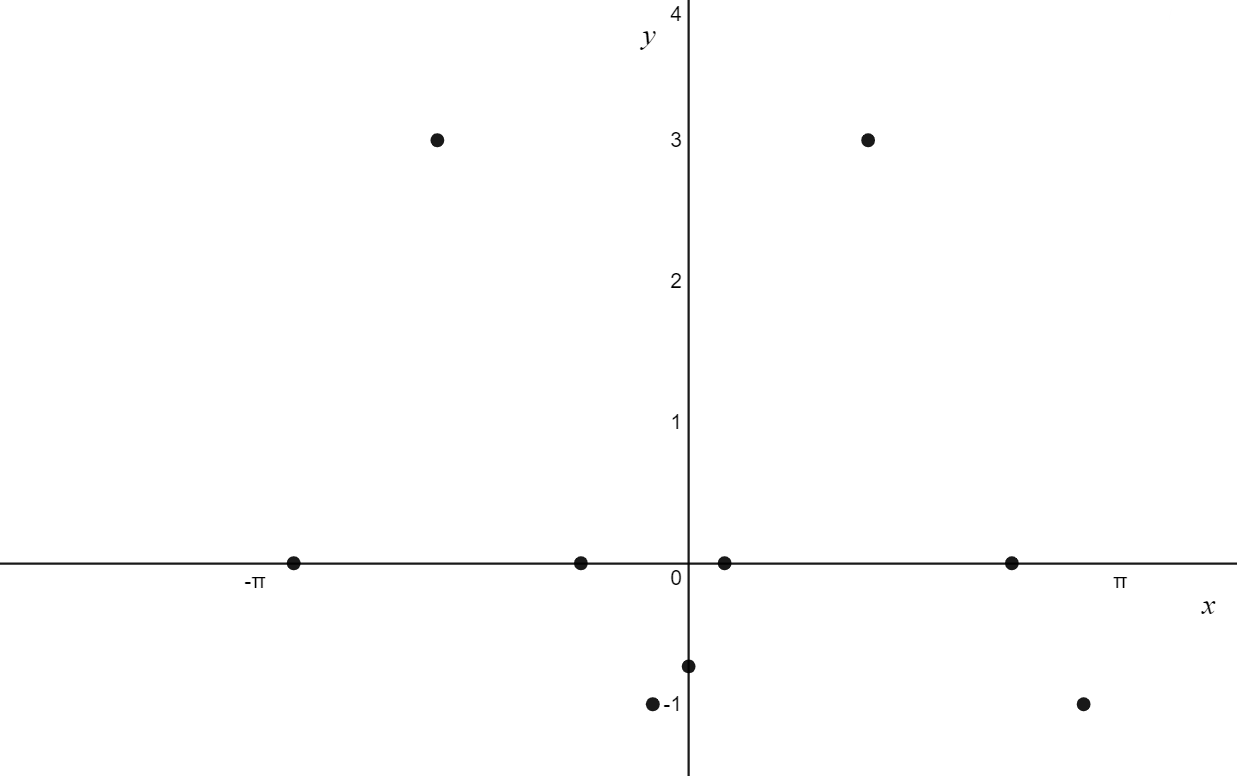
\[
\text{8. Endpoints} \\
\begin{aligned}
x&=-\pi\\
y &= 2\sin(2\cdot (-\pi)-\frac{\pi}{3})+1 \\
y &= 2\sin(-\frac{7\pi}{3}) + 1 \\
y&= 2 \cdot -\frac{\sqrt{3}}{2} + 1 \\
y&= -\sqrt{3} + 1 \\
\text{ }& \\
x&=\pi\\
y &= 2\sin(2\cdot (-\pi)-\frac{\pi}{3})+1 \\
y &= 2\sin(\frac{5\pi}{3}) + 1 \\
y&= 2 \cdot -\frac{\sqrt{3}}{2} + 1 \\
y&= -\sqrt{3} + 1 \\
\end{aligned}\\
\text{The endpoints are at } (-\pi, -\sqrt{3}+1), \, (\pi, -\sqrt{3}+1)
\]
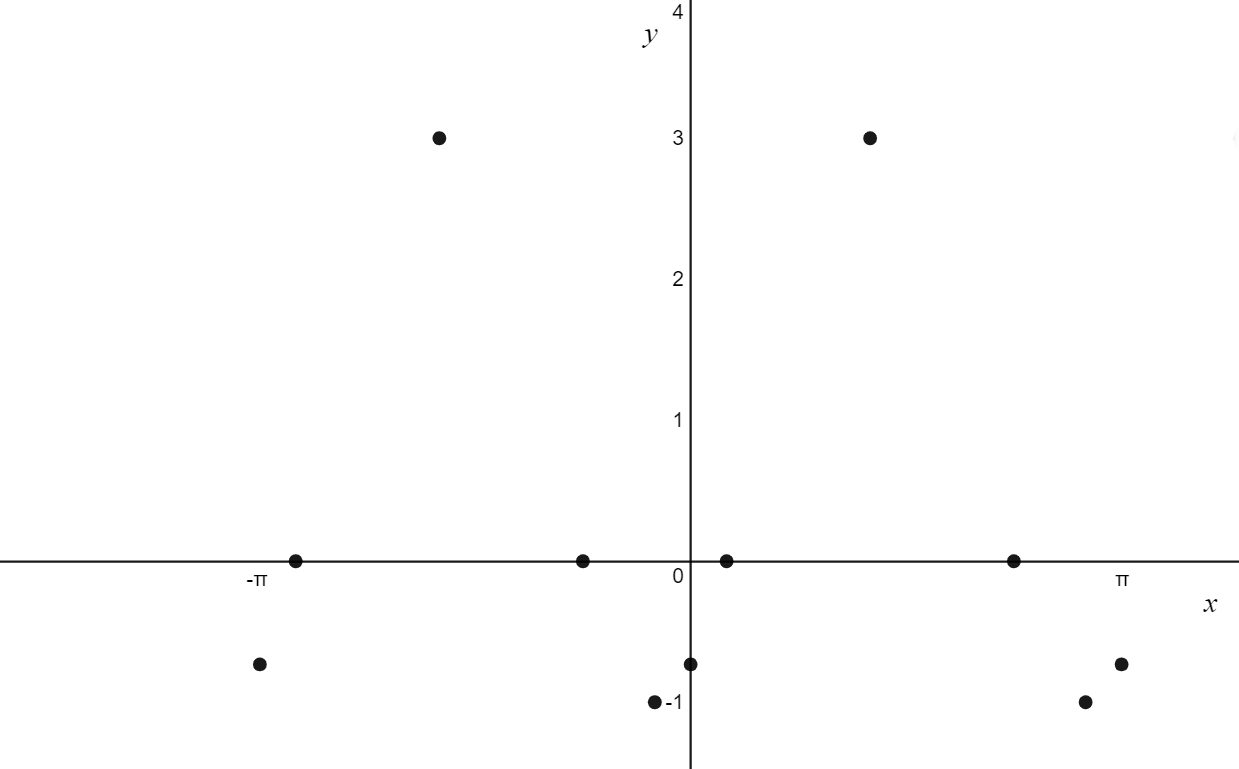
\[
\text{9. Connect the dots and label everything}
\]
\[
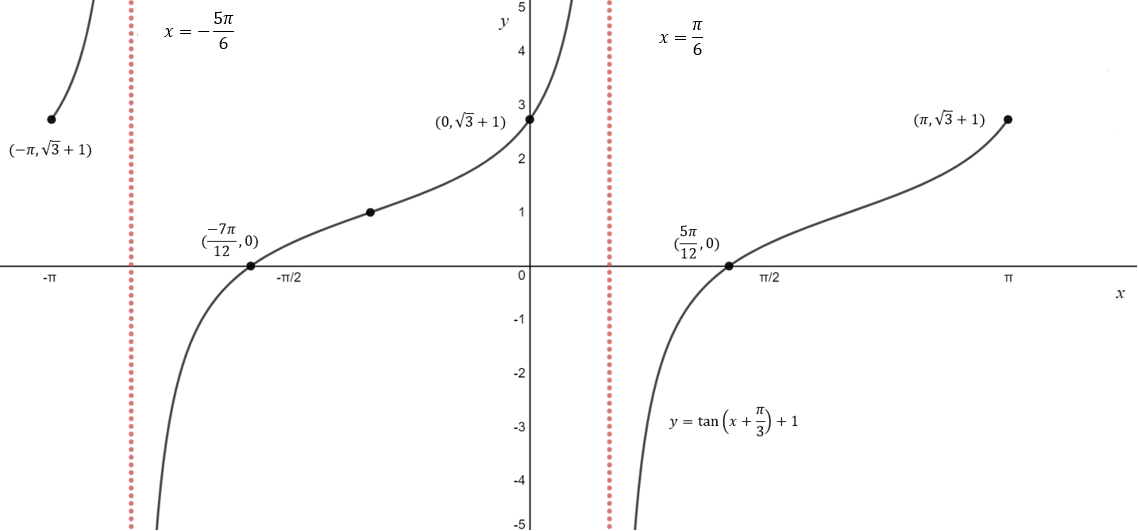
\text{Example 6.3: Sketch the graph of } y = \tan(x+\frac{\pi}{3})+1 \text{ for } x \in [-\pi, \pi]. \\
\text{Label the coordinates of any y-intercept, x-intercept, endpoints and the equations of any asymptotes.}
\]
\[
\text{1. y-intercept} \\
\begin{aligned}
x&=0\\
y &= \tan(0+\frac{\pi}{3})+1 \\
y&= (\sqrt{3})+1\\
y &=\sqrt{3}+1 \\
\end{aligned}\\
\text{There is a y-intercept at } (0, \sqrt{3}+1)
\]

\[
\text{2. X-intercepts} \\
\begin{aligned}
x\in[-\pi,\pi]\\
x + \frac{\pi}{3} &\in [-\frac{2\pi}{3}, \frac{4\pi}{3}] \\
\text{ } \\
0 &= \tan(x+\frac{\pi}{3})+1 \\
-1&=\tan(x+\frac{\pi}{3}) \\
\end{aligned}\\
\text{Basic Angle: } \frac{\pi}{4} \\
\text{Tan is negative in quadrant 2 and 4} \\
\text{ } \\
\begin{aligned}
\tan(\pi-\frac{\pi}{4}) &= \tan(\frac{3\pi}{4}) = -1 \\
\tan(2\pi - \frac{\pi}{4} &= \tan(\frac{7\pi}{4}) = -1 \\
\end{aligned}\\
\text{ } \\
\begin{aligned}
x + \frac{\pi}{3} &= \frac{3\pi}{4}, \frac{7\pi}{4}-2\pi \\
x&= \frac{9\pi}{12} - \frac{4\pi}{12}, -\frac{3\pi}{12} - \frac{4\pi}{12} \\
x&=\frac{5\pi}{12}, -\frac{7\pi}{12} \\
\end{aligned}\\
\text{There are x-intercepts at } (-\frac{7\pi}{12}, 0) \text{ and } (\frac{5\pi}{12}, 0)
\]
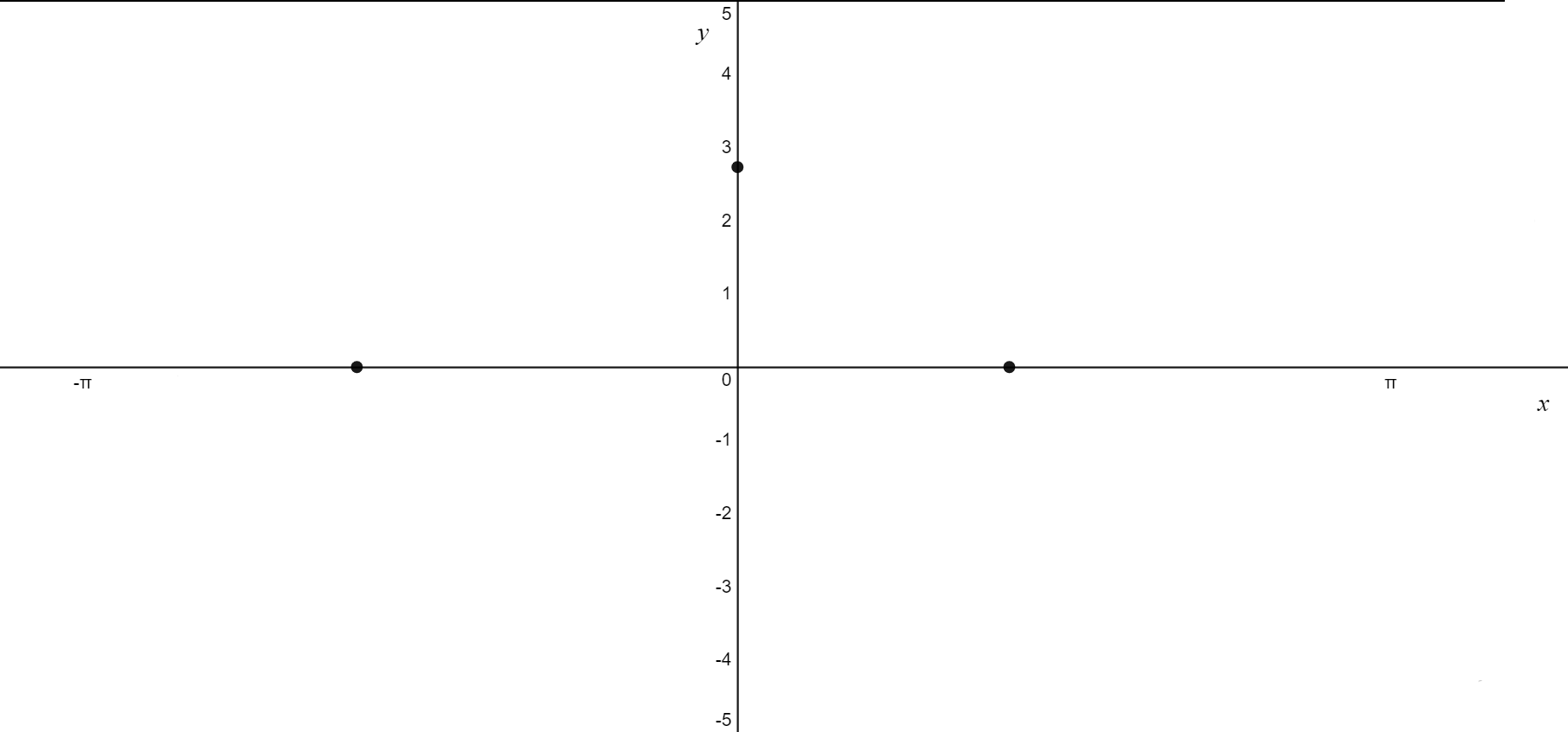
\[
\text{3. Asymptotes} \\
\begin{aligned}
x\in[-\pi,\pi]\\
x + \frac{\pi}{3} &\in [-\frac{2\pi}{3}, \frac{4\pi}{3}] \\
\text{ } \\
0 &= \cos(x+\frac{\pi}{3}) \\
\end{aligned}
\text{Basic Angle: } \frac{\pi}{2} \\
\begin{aligned}
\cos(\frac{\pi}{2}) &= 0 \\
\cos(\frac{3\pi}{2}) &= 0 \\
\end{aligned}\\
\text{ } \\
\begin{aligned}
x + \frac{\pi}{3} &= \frac{\pi}{2}, \frac{3\pi}{2}-2\pi \\
x&= \frac{3\pi}{6} - \frac{2\pi}{6},- \frac{3\pi}{6} - \frac{2\pi}{6} \\
x&=\frac{\pi}{6}, -\frac{5\pi}{6} \\
\end{aligned}\\
\text{The asymptotes have equations: } x = \frac{\pi}{6} \text{ and } x = -\frac{5\pi}{6}
\]

\[
\text{4. Asymptote midpoints} \\
\text{The asymptotes have equations: } x = \frac{\pi}{6} \text{ and } x = -\frac{5\pi}{6} \\
\text{The only pair of asymptotes which are next to each other are: }\frac{\pi}{6} \text{ and } -\frac{5\pi}{6} \\
\begin{aligned}
\frac{\frac{\pi}{6} + (-\frac{5\pi}{6})}{2} &= \frac{\frac{-4\pi}{6}}{2} \\
&= -\frac{2\pi}{6} \\
&= -\frac{\pi}{3} \\
\end{aligned}\\
\text{So, the point } (-\frac{\pi}{3}, 1) \text{ lies on the graph.}
\]
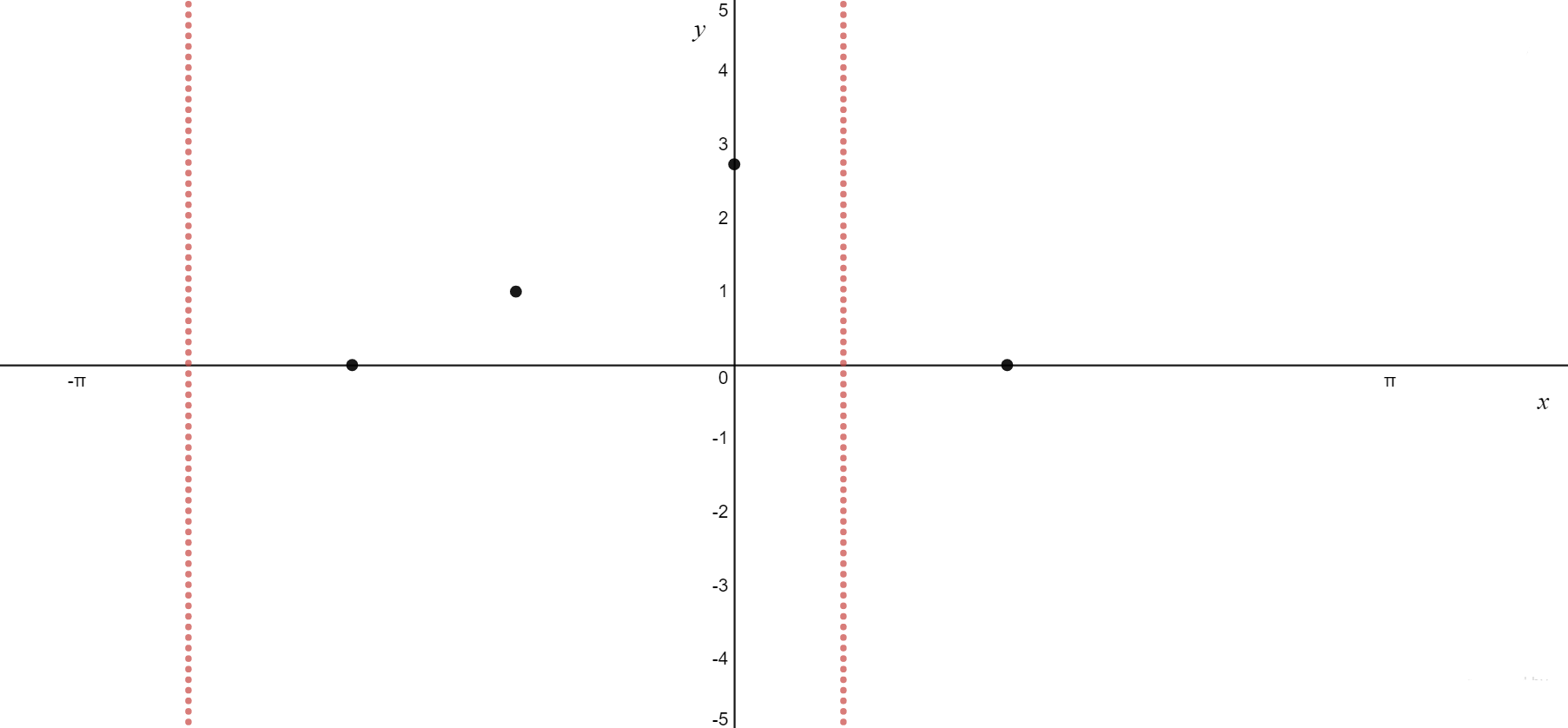
\[
\text{5. Endpoints} \\
\begin{aligned}
x&=-\pi\\
y &= \tan(-\pi+\frac{\pi}{3})+1\\
y &= \tan(\frac{-2\pi}{3})+1 \\
y&= \sqrt{3} + 1 \\
\text{ }& \\
x&=\pi\\
y &= \tan(\pi+\frac{\pi}{3})+1\\
y &= \tan(\frac{4\pi}{3})+1\\
y&= \sqrt{3} + 1 \\
\end{aligned}\\
\text{The endpoints are at } (-\pi, \sqrt{3}+1), \, (\pi, \sqrt{3}+1)
\]
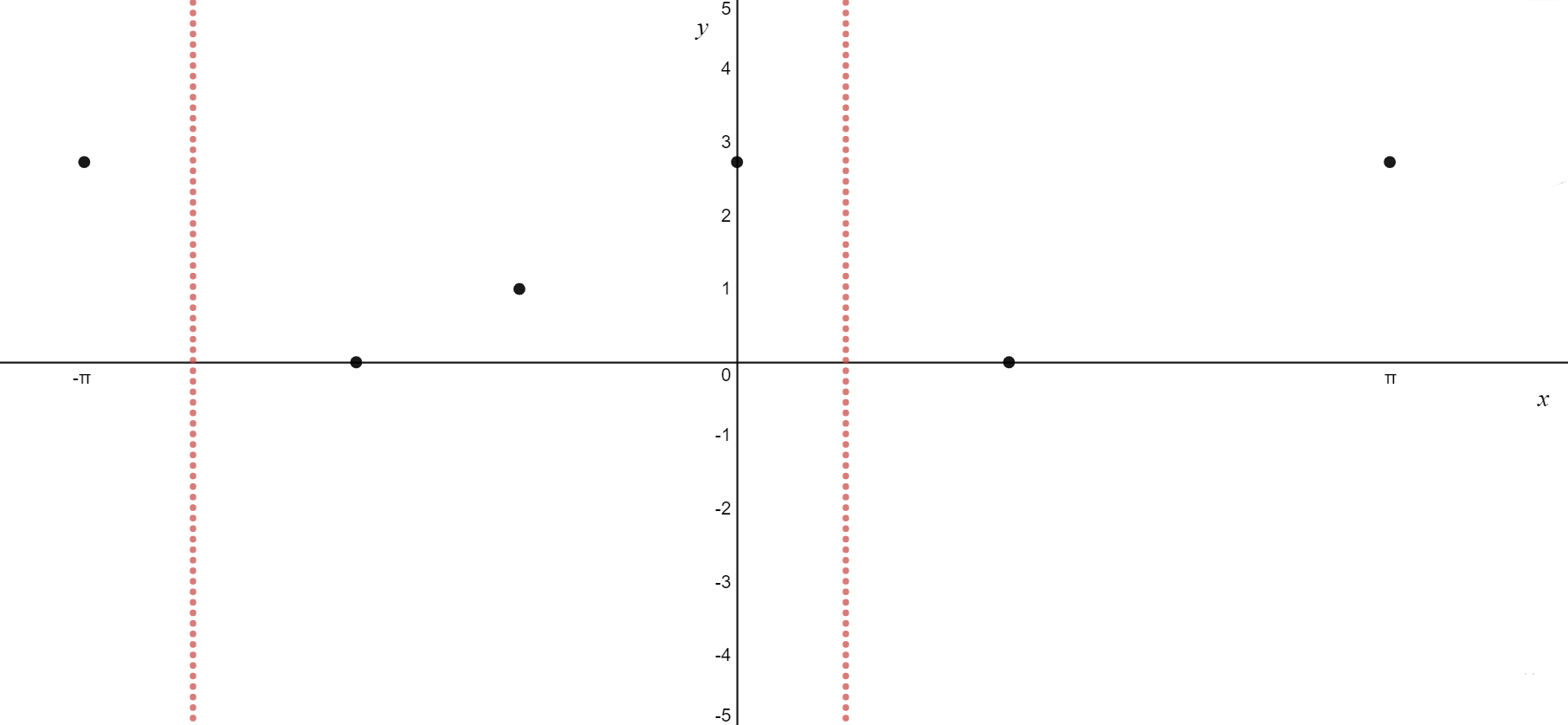
\[
\text{6. Connect the dots and label all necessary points}
\]
Solving trigonometric equations will seem quite difficult at first due to the large number of steps. It is important that you do it in a systematic manner. We have outlined the steps below and have provided a worked example.
| 1 | Adjust the domain provided to reflect the argument (stuff inside the sin/cos/tan function) of the trigonometric function (skip if finding general solutions) |
| 2 | Manipulate the equation so that it is of the form - sin(ax+b) = c, cos(ax+b) = c or tan(ax+b) = c |
| 3 | Assume that we are solving for sin(z) = |c|, cos(z) = |c| or tan(z) = |c| and find the value for z only thinking about the first quadrant. We will refer to this value z as the basic angle |
| 4 | Looking at the equations we got in step 2, think about which quadrants our solution(s) should be in. |
| 5 | Using supplementary angle formulae adjust the value for z so that you obtain two angles (between 0 and 2π which are in the quadrants determined in step 4. |
| 6 | ax+b will equal to the two values found in step 5. For general solutions simply add 2πk where k ∈ ℤ. For a given domain, add and/or subtract 2π from both angles listing all of the values obtainable within the domain found in step 1, NOT the domain provided in the question. |
| 7 | Subtract b and then divide by a for all values. |
\[ \text{Example 6.4: Solve } 2\sin(2(x-\frac{\pi}{6}))+1 = 0, x \in [-\pi, \pi]\\ \text{ }\\ \text{ }\\ \text{1. Adjust the domain}\\ 2\sin(2x-\frac{\pi}{3}) + 1 =0\\ \begin{aligned} x &\in [-\pi, \pi]\\ 2x &\in [-2\pi, 2\pi]\\ 2x - \frac{\pi}{3} &\in [-2\pi-\frac{\pi}{3}, 2\pi-\frac{\pi}{3}]\\ 2x - \frac{\pi}{3} &\in [-\frac{7\pi}{3}, \frac{5\pi}{3}]\\ \end{aligned}\\ \text{ }\\ \text{ }\\ \text{2. Rearrange the equation}\\ \begin{aligned} 2\sin(2(x-\frac{\pi}{6}))+1 &= 0\\ 2\sin(2x-\frac{\pi}{3}) + 1 &=0\\ \sin(2x-\frac{\pi}{3})&=-\frac{1}{2}\\ \end{aligned}\\ \text{ }\\ \text{ }\\ \text{3. Find the basic angle}\\ \sin(\frac{\pi}{6}) = \frac{1}{2}\\ \text{So, the basic angle is } \frac{\pi}{6}\\ \text{ }\\ \text{ }\\ \text{4. Identify the quadrants}\\ \sin(2x-\frac{\pi}{3})=-\frac{1}{2}\\ \text{Sine is only negative in quadrant 3 and 4.}\\ \text{ }\\ \text{ }\\ \text{5. Use supplementary angle formulae, after you get use to this process try and merge steps 5 and 6}\\ \text{Our basic angle is } \frac{\pi}{6}\\ \begin{aligned} \sin(\pi + \frac{\pi}{6}) &= \sin(2\pi - \frac{\pi}{6}) = -\frac{1}{2}\\ \sin(\frac{7\pi}{6}) &= \sin(\frac{11\pi}{6}) = -\frac{1}{2}\\ \end{aligned}\\ \text{ }\\ \text{ }\\ \text{6. Add and Subtract } 2\pi\\ \begin{aligned} 2x-\frac{\pi}{3} &= \frac{7\pi}{6}, \frac{7\pi}{6}-2\pi , \frac{11\pi}{6}-2\pi, \frac{11\pi}{6}-4\pi\\ 2x-\frac{\pi}{3} &= \frac{7\pi}{6}, -\frac{5\pi}{6} , -\frac{1\pi}{6}, -\frac{13\pi}{6}\\ \end{aligned}\\ \text{ }\\ \text{ }\\ \text{7. Solve for } x\\ \begin{aligned} 2x &= \frac{7\pi}{6}+\frac{\pi}{3}, -\frac{5\pi}{6}+\frac{\pi}{3} , -\frac{1\pi}{6}+\frac{\pi}{3}, -\frac{13\pi}{6}+\frac{\pi}{3}\\ 2x &= \frac{9\pi}{6}, -\frac{3\pi}{6}, \frac{1\pi}{6}, -\frac{11\pi}{6}\\ x &= \frac{9\pi}{12}, -\frac{3\pi}{12}, \frac{1\pi}{12}, -\frac{11\pi}{12}\\ x &= \frac{3\pi}{4}, -\frac{1\pi}{4}, \frac{1\pi}{12}, -\frac{11\pi}{12}\\ x &= -\frac{11\pi}{12}, -\frac{1\pi}{4}, \frac{1\pi}{12}, \frac{3\pi}{4}\\ \end{aligned}\\ \]
\[ \text{Example 6.5: Solve } 2\sin(2(x-\frac{\pi}{6}))+1 = 0 \text{ (Find the general solutions)}\\ \text{Steps 1-5 remain the same as the previous question.}\\ \sin(\frac{7\pi}{6}) = \sin(\frac{11\pi}{6}) = -\frac{1}{2} \text{ (Last line of step 5)}\\ \text{ }\\ \text{ }\\ \text{6. Add or subtract } 2\pi\\ 2x-\frac{\pi}{3} =\frac{7\pi}{6} + 2\pi k , \frac{11\pi}{6} + 2\pi k ,\, k \in \mathbb{Z}\\ \text{ }\\ \text{ }\\ \text{7. Solve for } x\\ \begin{aligned} 2x &=\frac{7\pi}{6} + \frac{\pi}{3} + 2\pi \cdot k , \frac{11\pi}{6} + \frac{\pi}{3} + 2\pi \cdot k , k \in \mathbb{Z}\\ 2x &=\frac{9\pi}{6} + 2\pi \cdot k , \frac{13\pi}{6} + 2\pi \cdot k , \,k \in \mathbb{Z}\\ x &=\frac{9\pi}{12} + \pi \cdot k , \frac{13\pi}{12} + \pi \cdot k , \,k \in \mathbb{Z}\\ \end{aligned} \]
Note: the textbook combines these two solutions into one (for cosmetic reasons I guess). This is unnecessary and should not be done. The reason being that if you happen to make a mistake when combining the two solutions you will lose 1 mark for no reason.
\[ \text{Example 6.6: Solve } \sqrt{3}\cos(2x)=\sin(2x) \text{ for } x \in [0, 2\pi]\\ \text{Step 1 Divide by cosine to get tan}\\ \begin{aligned} \frac{\sqrt{3}\cos(2x)}{\sqrt{3}\cos(2x)}&=\frac{\sin(2x)}{\sqrt{3}\cos(2x)}\\ \frac{\sin(2x)}{\sqrt{3}\cos(2x)}&=1\\ \frac{1}{\sqrt{3}}\tan(2x)&=1\\ \end{aligned} \text{ }\\ \text{ }\\ \text{Using the same process outlined above, you will get:}\\ x = \frac{\pi}{6} , \frac{2\pi}{3}, \frac{7\pi}{6}, \frac{5\pi}{3}\\ \]
The general form of sine, cosine and tangent functions are shown below. However, the question may provide us with the form we should use, this means that the equation provided may or may not have as many unknowns as the ones below. \[y = A\sin(nx+b)+c\] \[y = A\cos(nx+b)+c\] \[y = A\tan(nx+b)+c\] To find the value of any other unknowns, simply substitute the x and y-coordinates of any additional points provided into the equation (having found some unknowns as detailed below) and solve them (simultaneously).
For sine and cosine:
The value of A is the amplitude - half the vertical distance from peak to trough.
The value of n can be calculated by examining the period of the function.
\[\frac{2\pi}{n} = \text{period}\ \rightarrow n = \frac{2\pi}{\text{period}}\]
The value of c will be the value of the y-intercept of the centreline (the horizontal line which lies in between the peaks and troughs).
To find the value of b use the additional point provided. When solving the equation simply find any two consecutive solutions.
For tangent
The value of n can be calculated by examining the period of the function.
\[\frac{\pi}{n} = \text{period}\ \rightarrow n = \frac{\pi}{\text{period}}\]
Asymptotes will be present when \(\cos(nx+b) = 0\). Substituting in the x-intercept value of the asymptotes may allow you to find the value for n or b